KMP算法
把 KMP 算法做个详细总结,写成博文。
主要分为四个部分:
-
KMP 中的前缀后缀
-
构建 Next数组
-
KMP算法匹配过程
-
源码示例.
KMP 中的前缀后缀
我们以字符串 match = "12312" 为例。它的前缀指的是: 1, 12, 123, 1231。它的后缀指的是: 2, 12, 312, 2312。
KMP 中需要预先计算字符串 最长相同前后缀的长度,用于加快比对过程,具体原理第三部分详细说明。
这个 最长相同前后缀的长度 保存在一个数组中,这就是我们要找的 Next 数组。Next[i] 表示的意思是:match[0] ~ match[i]这个子串 的 最长相同前后缀的长度。
比如: i = 3, 则表示 "1231" 这个字符串的 最长相同前后缀的长度,本例中值为 1。 (前缀 "1", 后缀 "1")
如何构建 Next 数组
构建 Next 数组的过程是一个递推的过程,即 Next[i] 的值的得到依赖于 Next[0 ~ i-1] 的信息。
我们边遍历 match 字符串,边构建 Next数组,其中Next[0] = 0。
假设当前我们遍历到了第 i 个字符,且 Next[i -1] = k;
图片中实线线段代表已经遍历了的字符,虚线表示还没有遍历到的字符,括号选取的为相同的前后缀:
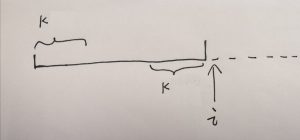
由此,我们可以轻易的看出,若 match[k] == match[i], 那么 Next[i] = k + 1; 若 match[k] != match[i] 呢?我们就需要再往前推。
假设 Next[k - 1] = m, 则情况如下图所示,我们只需要继续比较 match[m] == match[i],若相等则说明 match[i] = m + 1,若不相等则 继续往前推 (match[m - 1]),直到相等或者match[某值] = 0 为止。
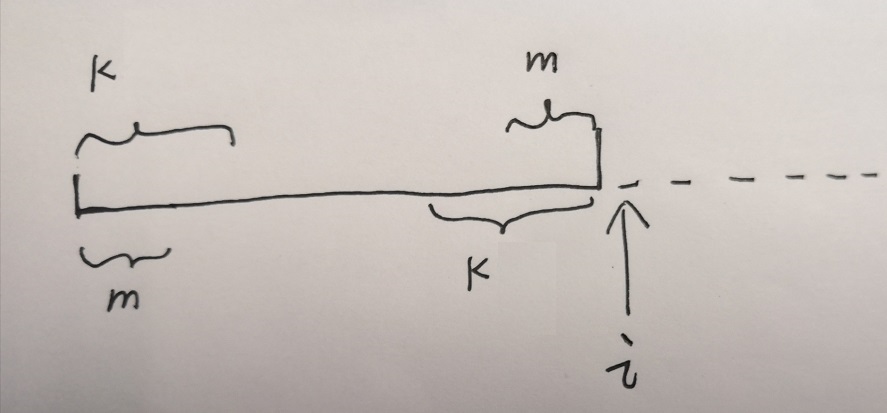
由此,递推构建出了 Next 数组。
KMP 算法过程
我们以 input = "1231412312", match = "12312" 为例来讨论 KMP算法。设 i 为 input 的下标,j 为 match 的下标。
逐字符比对,直到找到一个不相等的字符,如下图所示:
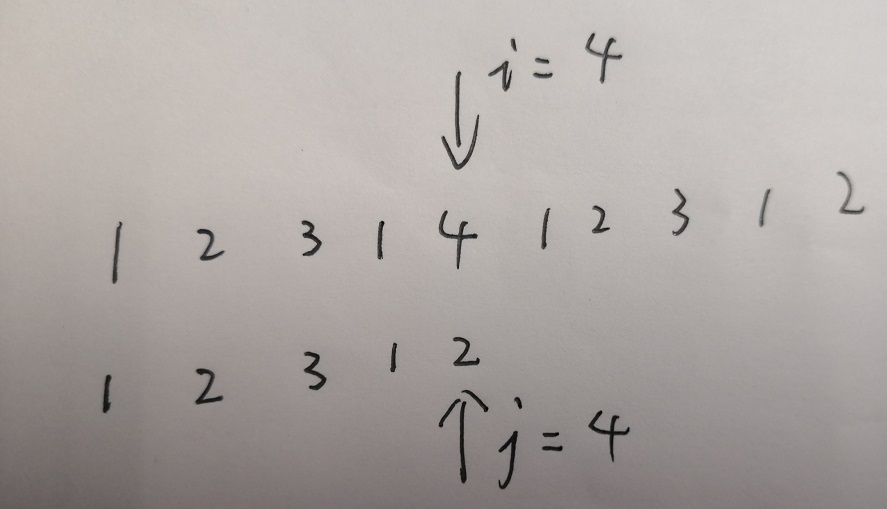
这时,我们需要找一个位置重新开始比较字符串,那么找哪个位置呢?
显然,如果 已经比较成功的后缀 有一段 前缀 和它相同,那么就不用重复比较了,直接从 相同前缀 之后的位置开始重新比较就可。这时候就可以看出我们之前找 最长相同前后缀的长度 的意义了。本例中 Next[j - 1] = 1,则下一次开始的位置为比较 match[1] 和 input[i]。
后面的过程,就简单了,即逐字符比对,遇到不匹配的则从 j = Next[j - 1]的位置开始重新比对,直到字符串遍历完毕。
完整实现
以下奉上 C++ 实现的 KMP 算法. 输出为所有匹配成功的第一个字符位置。
测试用例:
输入string input = "kmpmpmmkmpkmpmmkmpmkmmmpkmpmmkmpmppp";
string match = "kmpmmkmpm";
输出[10, 24]
vector<int> makeNext(string &base){
vector<int> next(base.size(), 0);
for(int i = 1; i < base.size(); ++i){
int k = next[i - 1];
while(k > 0 && base[k] != base[i])
k = next[k - 1];
if (base[k] == base[i])
next[i] = ++k;
}
return next;
}
vector<int> kmpMatch(string &input, string &match){
vector<int> next = makeNext(match);
vector<int> matchIndexs;
// i 为 input下标, j 为 match下标
int i = 0, j = 0;
while (i < input.size()){
if (input[i] == match[j]){
++i;
++j;
if (j == match.size()){
matchIndexs.push_back(i - match.size());
j = next[j - 1];
}
}else{
if (j == 0)
++i;
else
j = next[j - 1];
}
}
return matchIndexs;
}